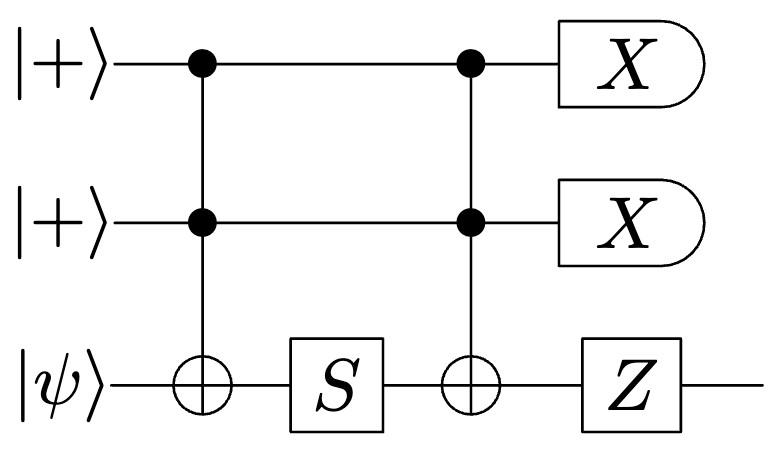
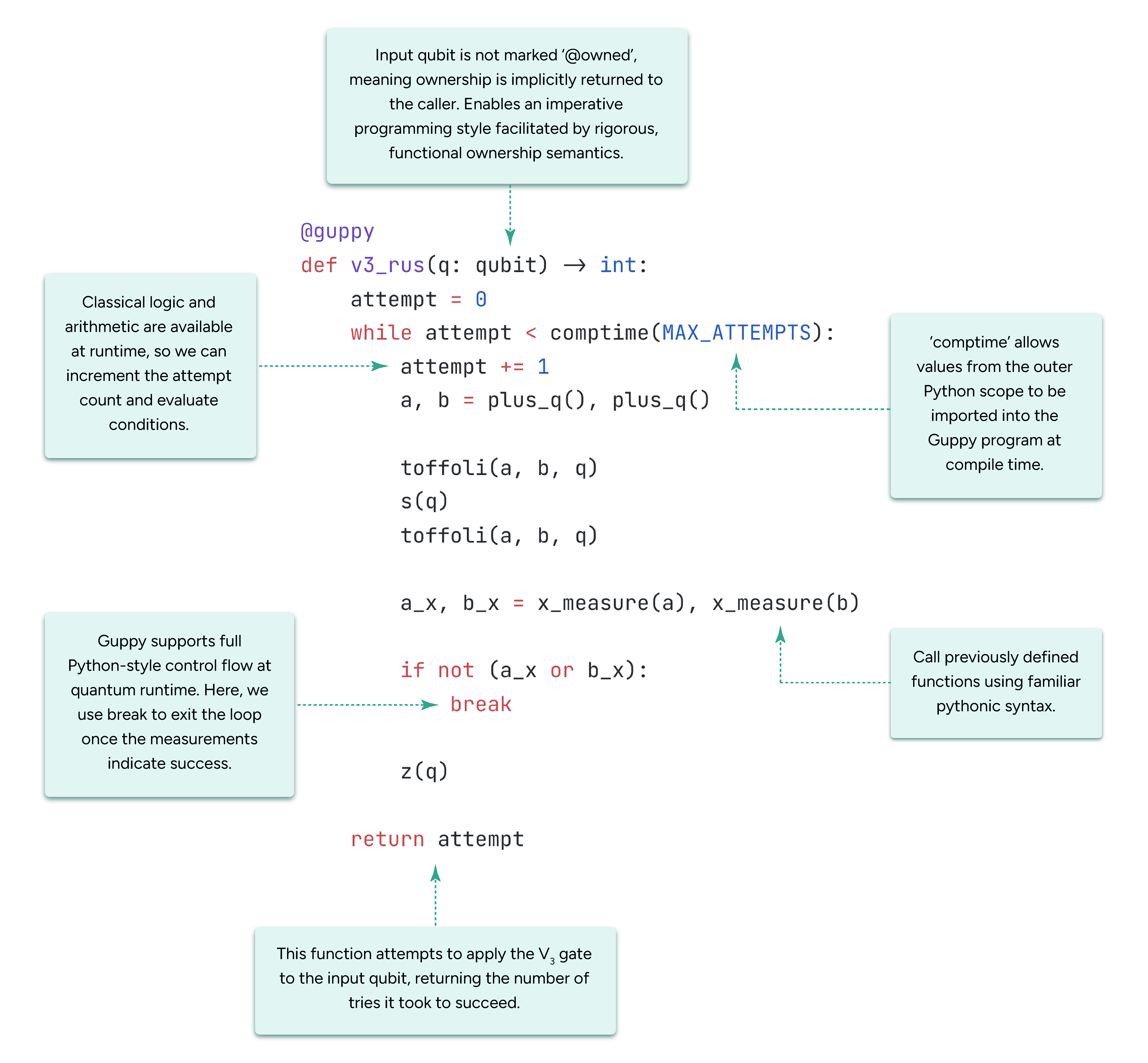
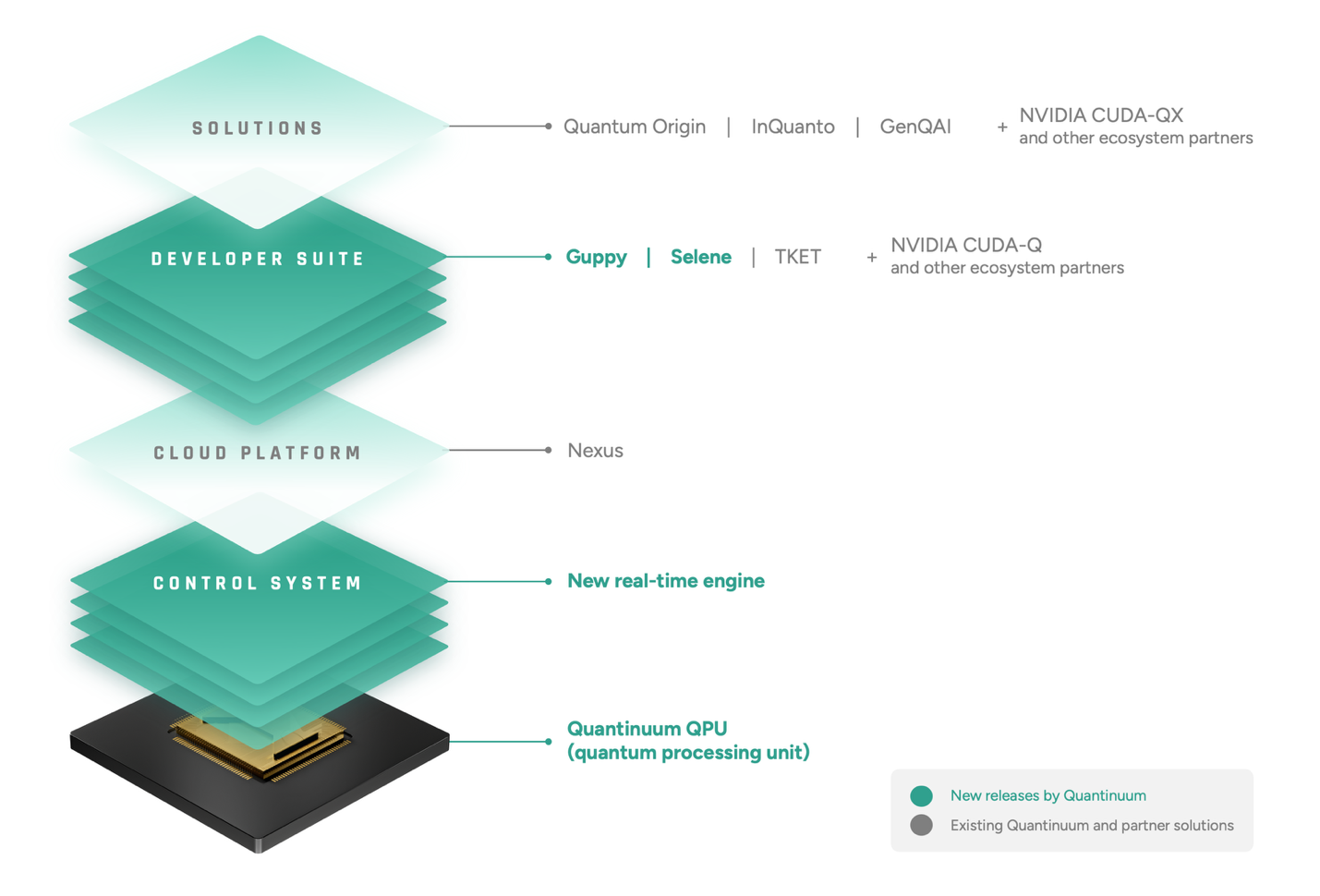
From machine learning to quantum physics, tensor networks have been quietly powering the breakthroughs that will reshape our society. Originally developed by the legendary Nobel laureate Roger Penrose, they were first used to tackle esoteric problems in physics that were previously unsolvable.
Today, tensor networks have become indispensable in a huge number of fields, including both classical and quantum computing, where they are used everywhere from quantum error correction (QEC) decoding to quantum machine learning.
In , we teamed up with luminaries from the University of British Columbia, California Institute of Technology, University of Jyväskylä, KBR Inc, NASA, Google Quantum AI, NVIDIA, JPMorgan Chase, the University of Sherbrooke, and Terra Quantum AG to provide a comprehensive overview of the use of tensor networks in quantum computing.
Standing on the shoulders of giants
Part of what drives our leadership in quantum computing is our commitment to building the best scientific team in the world. This is precisely why we hired Dr. Reza Haghshenas, one of the world’s leading experts in tensor networks, and a co-author on the paper.
Dr. Haghshenas has been researching tensor networks for over a decade across both academia and industry. Dr. Haghshenas did postdoctoral work under , a leading figure in the use of tensor networks for quantum physics and chemistry.
“Working with Dr. Garnet Chan at Caltech was a formative experience for me”, remarked Dr. Haghshenas. “While there, I contributed to the development of quantum simulation algorithms and advanced classical methods like tensor networks to help interpret and simulate many-body physics.”
Since joining “π…´÷±≤•, Dr. Haghshenas has led projects that bring tensor network methods into direct collaboration with experimental hardware teams ‚Äî exploring quantum magnetism on real quantum devices and helping demonstrate early signs of quantum advantage. He also contributes to , helping the broader research community access these methods.
Dr. Haghshenas’ work sits in a broad and vibrant ecosystem exploring novel uses of tensor networks. Collaborations with researchers like Dr. Chan at Caltech, and NVIDIA have brought GPU-accelerated tools to bear on the forefront of applying tensor networks to quantum chemistry, quantum physics, and quantum computing.
A powerful simulation tool
Of particular interest to those of us in quantum computing, the best methods (that we know of) for simulating quantum computers with classical computers rely on tensor networks. Tensor networks provide a nice way of representing the entanglement in a quantum algorithm and how it spreads, which is crucial but generally quite difficult for classical algorithms. In fact, it’s partly tensor networks’ ability to represent entanglement that makes them so powerful for quantum simulation. Importantly, it is our in-house expertise with tensor networks that makes us confident we are indeed moving past classical capabilities.
A theory of evolution
Tensor networks are not only crucial to cutting-edge simulation techniques. ¬ÝAt “π…´÷±≤•, we're working on understanding and implementing quantum versions of classical tensor network algorithms, from quantum matrix product states to holographic simulation methods. In doing this, we are leveraging decades of classical algorithm development to advance quantum computing.
A topic of growing interest is the role of tensor networks in QEC, particularly in a process known as decoding. QEC works by encoding information into an entangled state of multiple qubits and using syndrome measurements to detect errors. These measurements must then be decoded to identify the specific error and determine the appropriate correction. This decoding step is challenging—it must be both fast (within the qubit’s coherence time) and accurate (correctly identifying and fixing errors). Tensor networks are emerging as one of the most for tackling this task.
Looking forward (and backwards, and sideways...)
Tensor networks are more than just a powerful computational tool — they are a bridge between classical and quantum thinking. As this new paper shows, the community’s understanding of tensor networks has matured into a robust foundation for advancing quantum computing, touching everything from simulation and machine learning to error correction and circuit design.
At “π…´÷±≤•, we see this as an evolutionary step, not just in theory, but in practice. By collaborating with top minds across academia and industry, we're charting a path forward that builds on decades of classical progress while embracing the full potential of quantum mechanics. This transition is not only conceptual but algorithmic, advancing how we formulate and implement methods utilizing efficiently both classical and quantum computing. Tensor networks aren‚Äôt just helping us keep pace with classical computing; they‚Äôre helping us to transcend it.